단어를 벡터로 표현하는 방법은 지금까지 활발히 연구되었습니다. 그중에서도 성공적인 기법들을 크게 두 부류로 나눌 수 있는데, 바로 ‘통계 기반 기법’과 ‘추론 기반 기법’입니다. 단어의 의미를 얻는 방식은 서로 크게 다르지만, 그 배경에는 모두 분포 가설이 있습니다. 이번 절에서는 통계 기반 기법의 문제를 지적하고, 그 대안인 추론 기반 기법의 이점을 거시적 관점에서 설명합니다. 그런 다음 word2vec의 전처리를 위해 신경망으로 ‘단어’를 처리하는 예를 보여드리겠습니다.
1. 통계 기반 기법의 문제점
지금까지 본 것처럼 통계 기반 기법에서는 주변 단어의 빈도를 기초로 단어를 표현했습니다. 구체적으로는 단어의 동시발생 행렬을 만들고 그 행렬에 SVD를 적용하여 밀집벡터(단어의 분산 표현)를 얻었습니다. 그러나 이 방식은 대규모 말뭉치를 다룰 때 문제가 발생합니다. 현업에서 다루는 말뭉치의 어휘 수는 어마어마합니다. 예컨대 영어의 어휘 수는 100만을 훌쩍 넘는다고 합니다. 어휘가 100만 개라면, 통계 기반 기법에서는 ‘100만×100만’이라는 거대한 행렬을 만들게 됩니다. 이런 거대 행렬에 SVD를 적용하는 일은 현실적이지 않겠죠.
NOTE_ SVD를 n×n 행렬에 적용하는 비용은 O(n3 )입니다. O(n3 )이란 계산 시간이 n의 3 제곱에 비례한다는 뜻입니다. 슈퍼컴퓨터를 동원해도 처리할 수 없는 수준이죠. 실제로는 근사적인 기법과 희소행렬의 성질 등을 이용해 속도를 개선할 수 있습니다만, 그렇다고 해도 여전히 상당한 컴퓨팅 자원을 들여 장시간 계산해야 합니다.
통계 기반 기법은 말뭉치 전체의 통계(동시발생 행렬과 PPMI 등)를 이용해 단 1회의 처리 (SVD 등)만에 단어의 분산 표현을 얻습니다. 한편, 추론 기반 기법에서는, 예컨대 신경망을 이용하는 경우는 미니배치로 학습하는 것이 일반적입니다. 미니배치 학습에서는 신경망이 한 번에 소량(미니배치)의 학습 샘플씩 반복해서 학습하며 가중치를 갱신해갑니다. [그림 1] 은 이 두 기법의 큰 차이를 보여줍니다.
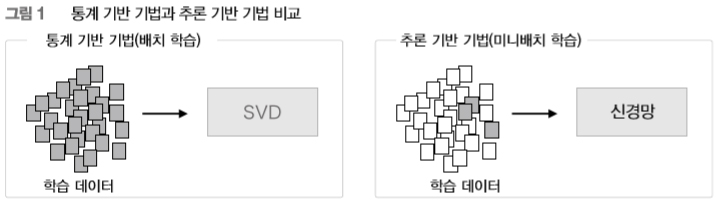
[그림 1]처럼 통계 기반 기법은 학습 데이터를 한꺼번에 처리합니다(배치 학습). 이에 반해 추론 기반 기법은 학습 데이터의 일부를 사용하여 순차적으로 학습합니다(미니배치 학습). 이 말은 말뭉치의 어휘 수가 많아 SVD 등 계산량이 큰 작업을 처리하기 어려운 경우에도 신경망을 학습시킬 수 있다는 뜻입니다. 데이터를 작게 나눠 학습하기 때문이죠. 게다가 여러 머신과 여러 GPU를 이용한 병렬 계산도 가능해져서 학습 속도를 높일 수도 있습니다. 추론 기반 기법이 큰 힘을 발휘하는 영역이죠. 추론 기반 기법이 통계 기반 기법보다 매력적인 점은 이 외에도 더 있습니다.
2. 추론 기반 기법 개요
추론 기반 기법에서는 당연히 ‘추론’이 주된 작업입니다. 추론이란 [그림 2]처럼 주변 단어(맥락)가 주어졌을 때 “?”에 무슨 단어가 들어가는지를 추측하는 작업입니다.

[그림 2]처럼 추론 문제를 풀고 학습하는 것이 ‘추론 기반 기법’이 다루는 문제입니다. 이러한 추론 문제를 반복해서 풀면서 단어의 출현 패턴을 학습하는 것이죠. ‘모델 관점’에서 보면, 이 추론 문제는 [그림 3]처럼 보입니다.
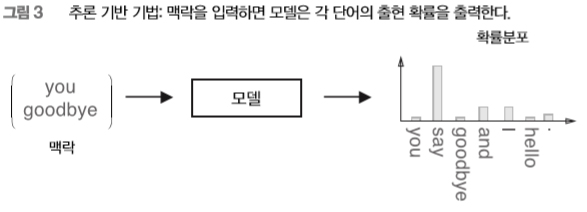
[그림 3]처럼 추론 기반 기법에는 어떠한 모델이 등장합니다. 우리는 이 모델로 신경망을 사용합니다. 모델은 맥락 정보를 입력받아 (출현할 수 있는) 각 단어의 출현 확률을 출력합니다. 이러한 틀 안에서 말뭉치를 사용해 모델이 올바른 추측을 내놓도록 학습시킵니다. 그리고 그 학습의 결과로 단어의 분산 표현을 얻는 것이 추론 기반 기법의 전체 그림입니다.
NOTE_ 추론 기반 기법도 통계 기반 기법처럼 분포 가설에 기초합니다. 분포 가설이란 ‘단어의 의미는 주변 단어에 의해 형성된다’는 가설로, 추론 기반 기법에서는 이를 앞에서와 같은 추측 문제로 귀결시켰습니다. 이처럼 두 기법 모두 분포 가설에 근거하는 ‘단어의 동시발생 가능성’을 얼마나 잘 모델링하는가가 중요한 연구주제입니다.
3. 신경망에서의 단어 처리
지금부터 신경망을 이용해 ‘단어’를 처리합니다. 그런데 신경망은 “you”와 “say” 등의 단어를 있는 그대로 처리할 수 없으니 단어를 ‘고정 길이의 벡터’로 변환해야 합니다. 이때 사용하는 대표적인 방법이 단어를 원핫one-hot 표현(또는 원핫 벡터)으로 변환하는 것입니다. 원핫 표현이란 벡터의 원소 중 하나만 1이고 나머지는 모두 0인 벡터를 말합니다. 원핫 표현에 대해 구체적으로 살펴봅시다. 여기에서는 앞 장과 같이 “You say goodbye and I say hello.”라는 한 문장짜리 말뭉치를 예로 설명하겠습니다. 이 말뭉치에는 어휘가 총 7개 등장합니다(“you”, “say”, “goodbye”, “and”, “i”, “hello”, “.”). 이중 두 단어의 원핫 표현을 [그림 4]에 나타내봤습니다.
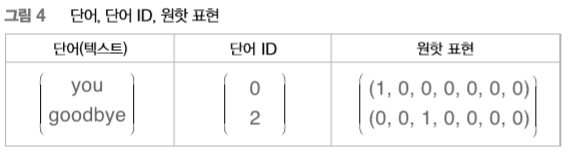
[그림 4]처럼 단어는 텍스트, 단어 ID, 그리고 원핫 표현 형태로 나타낼 수 있습니다. 여기서 단어를 원핫 표현으로 변환하는 방법은 이렇습니다. 먼저 총 어휘 수만큼의 원소를 갖는 벡터를 준비하고, 인덱스가 단어 ID와 같은 원소를 1로, 나머지는 모두 0으로 설정합니다. 이처럼 단어를 고정 길이 벡터로 변환하면 우리 신경망의 입력층은 [그림 5]처럼 뉴런의 수를 ‘고정’할 수 있습니다.

[그림 5]처럼 입력층의 뉴런은 총 7개입니다. 이 7개의 뉴런은 차례로 7개의 단어들에 대응합니다(첫 번째 뉴런은 “you”에, 두 번째 뉴런은 “say”에, ...). 이제 이야기가 간단해졌습니다. 단어를 벡터로 나타낼 수 있고, 신경망을 구성하는 ‘계층’들은 벡터를 처리할 수 있습니다. 다시 말해, 단어를 신경망으로 처리할 수 있다는 뜻이죠. 예컨대 [그림 3-6]은 원핫 표현으로 된 단어 하나를 완전연결계층을 통해 변환하는 모습을 보여줍니다.
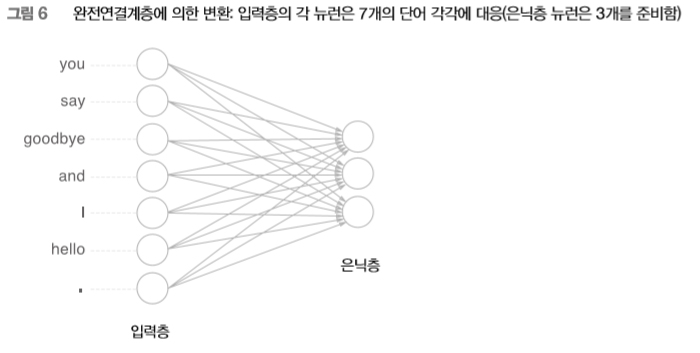
[그림 6]의 신경망은 완전연결계층이므로 각각의 노드가 이웃 층의 모든 노드와 화살표로 연결되어 있습니다. 이 화살표에는 가중치(매개변수)가 존재하여, 입력층 뉴런과의 가중합weighted sum이 은닉층 뉴런이 됩니다. 참고로 이번 장에서 사용하는 완전연결계층에서는 편향을 생략했습니다(이 부분은 뒤의 word2vec 설명 때 이야기하겠습니다).
WARNING_ 편향을 이용하지 않는 완전연결계층은 ‘행렬 곱’ 계산에 해당합니다. 그래서 이 책의 경우, 완전연결계층은 1장에서 구현한 MatMul 계층과 같아지죠. 참고로 딥러닝 프레임워크들은 일반적으로 완전연결계층을 생성할 때 편향을 이용할지 선택할 수 있도록 해줍니다.
자, [그림 6]에서는 뉴런 사이의 결합을 화살표로 그렸습니다만, 이후로는 가중치를 명확하게 보여주기 위해 [그림 7]처럼 그리겠습니다.
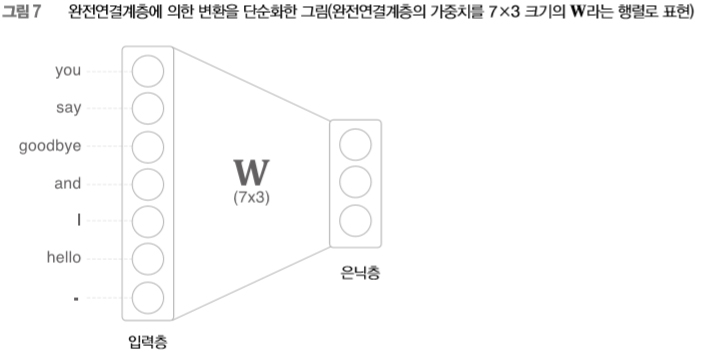
그럼, 여기까지의 이야기를 코드로 살펴보고 갑시다. 거두절미하고, 지금의 완전연결계층에 의한 변환은 파이썬으로는 다음과 같이 작성할 수 있습니다.

이 코드는 단어 ID가 0인 단어를 원핫 표현으로 표현한 다음 완전연결계층을 통과시켜 변환하는 모습을 보여줍니다. 복습해보자면, 완전연결계층의 계산은 행렬 곱으로 수행할 수 있고, 행렬 곱은 넘파이의 np.matmul( )이 해결해줍니다(편향은 생략).
WARNING_ 이 코드에서 입력 데이터(c)의 차원 수(ndim)는 2입니다. 이는 미니배치 처리를 고려한 것으로, 최초의 차원(0번째 차원)에 각 데이터를 저장합니다.
앞의 코드에서 주목할 곳은 c와 W의 행렬 곱 부분입니다. 자, c는 원핫 표현이므로 단어 ID에 대응하는 원소만 1이고 그 외에는 0인 벡터입니다. 따라서 앞 코드의 c와 W의 행렬 곱은 결국 [그림 8]처럼 가중치의 행벡터 하나를 ‘뽑아낸’ 것과 같습니다.
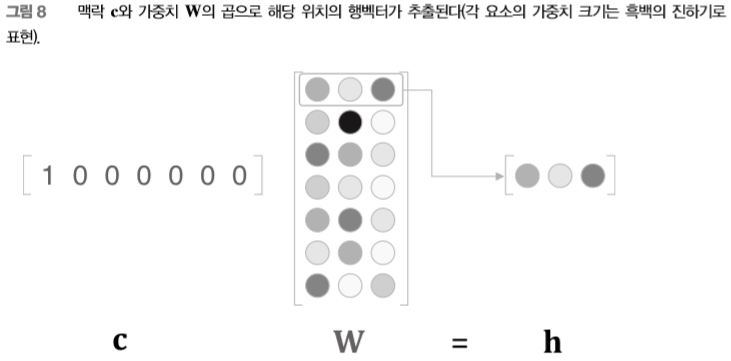
그저 가중치로부터 행벡터를 뽑아낼 뿐인데 행렬 곱을 계산하는 건 비효율적이라고 생각되시죠? 이 점은 ‘4.1 word2vec 개선 ①’ 절에서 개선할 예정입니다. 또한, 앞의 코드로 수행한 작업은 (1장에서 구현한) MatMul 계층으로도 수행할 수 있습니다. 다음 코드처럼 말이죠.

이 코드는 common 디렉터리에 있는 MatMul 계층을 임포트하여 사용합니다. 그런 다음 MatMul 계층에 가중치 W를 설정하고 forward( ) 메서드를 호출해 순전파를 수행합니다.
이전 글 : 내일의 오픈소스 프로젝트가 인터페이스일 수 있는 이유
다음 글 : 버그헌팅 프로그램을 하기 전에 '윤리'
최신 콘텐츠